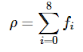This is a Lattice Boltzmann fluid simulation implemented in (unoptimized) JavaScript. Graphics is handled using the p5.js library and the lodash library is used for deep cloning an array of objects. A short clip showing a planar obstacle shedding vortices is presented below:
The details:
I'd been watching Prof. Patrick Winston's MIT OpenCourseware lectures on Artificial Intelligence ~last month. As a result, I started searching for related stuff on YouTube, Coursera, edX and the like. In the process, I guess being bombarded by recommendations and suggestions from these sites on a great breadth of subjects, I got interested in simulating(and visualizing) physical processes often represented by differential equations. I'm not totally certain why I gravitated towards it but it's probably because of how accessible that seemed at the time - aside from the obvious reason of it being a field very familiar to me - and it had been a while that I had written code, I guess I wanted a hit. So, I started with the 3 body problem. That was trivial to implement and it was done and dusted in a matter of hours. Then I went on to the 1-D heat/diffusion equation. While the Finite Difference implementation of the PDE was simple enough to be worked out on a spreadsheet, I really enjoyed the insightful conservation-law based derivation that took me down a rabbit hole of transport phenomena.
After my interest faded from the heat equation, I turned towards the Navier-Stokes equations - after all, they were in the same class of problems as the heat equation, only more universal; and if I could simulate the NS equations, I would be able to make some cool-looking fluid animations. After tinkering around some, to my disappointment, I found out that the pressure term had no obvious solution. This shoved me towards another engrossing journey. For the supposed civil engineer that I am, it was embarrassing that I had no idea that the study of simulating the Navier-Stokes equation was in itself a huge, distinct field owing, in part, to the difficulty arising from the pressure term - I should've known at least that much. Much YouTube and Google searches went into understanding some of the workarounds that people seemed to have come up with over the years - vorticity-streamfunction and artificial compressibility methods are the two I remember. NPTEL's course on Computational Fluid Dynamics was really helpful. Sure, I understood better what beast I was dealing with, but the deeper you gauge, the darker the abyss looks. I just knew there were going to be a lot of headaches down the road. Presumably, one had to use staggered grid to avoid numerical instabilities, putting that down in code I didn't know how it was going to look like. Similarly there was the complication that boundary conditions for obstacles to the flow and the computation domain could pose. And all that trouble would be for naught if the computation proved to be too CPU-intensive to run a simple demonstration on a regular PC. Giving up on the idea aside, I did learn here what on earth I'd been taught in modelling the Debris Flow phenomenon in Water Induced Hazards curriculum of Water Resources Engineering. Terminologies such as 'upwind scheme', 'staggered grid', 'vector and scalar points' made a lot more sense after this. I wish I'd been given more explanation regarding the matter in class. Amazing how internet doesn't really give you an easy answer for whatever you have to throw at it. Niche topics have niche search results no matter how close they actually are to a wildly popular counterpart. Anyway, I did learn the modern scene of fluid simulation from the experience. I got to know that creating physically accurate fluid models for real-life engineering and scientific tasks takes a lot of computational effort and rigor and that simulation for the visual appeal alone for the field of computer graphics has been figured out fairly recently: Jos Stam's approach comes to mind. The derivation of and an approach to simulating the NS equations also taught me a few things about vector fields and linear algebra, such as the now-obvious-seeming Helmholtz decomposition theorem.
Anyway, after exploration of the NS equations, the magic of the internet gently pushed me towards another way to do fluid simulations. Enter, Lattice Boltzmann Method. This technique doesn't bother with the NS equations at all. Instead of trying to discretize and solve a PDE for macroscopic variables: velocity and the pressure, the LBM works from the bottom up. It recognizes that the continuous-seeming macroscopic properties emerge out of the microscopic phenomena of molecular activities. So, the LBM, it seems, is based on the Kinetic Theory and statistical mechanics. Now statistical mechanics isn't something I studied in university so it's not a subject that I'm comfortable working with, but upon typing the term "Lattice Boltzmann simulation" on YouTube, I saw numerous videos that made it seem so easy to simulate a flowing fluid. I thus set out on implementing my own version of the LBM. There was a lot of good content on the internet, from YouTube videos to free online courses on Coursera. I also referred to multiple books and texts on the subject. Among them, the Coursera course on Simulation and Modeling of natural processes from the University of Geneva and the books: [ a) Lattice Boltzmann Modeling - An introduction to geoscientists and engineers by Michael C. Sukop and Daniel T. Thorne, b) The Lattice Boltzmann Method - Principles and Practice by Timm Kruger, Halim Kusumaatmaja et al, c) A Practical Introduction to Lattice Boltzmann Method by Alexander J. Wagner, and d) Review of Boundary Conditions and Investigation Towards the Development of a Growth Model: a Lattice Boltzmann Method Approach (Doctoral Thesis) by Albert Puig Aranega ] and a classroom handout(I believe) and a live simulation webpage by Prof. Dan Schroeder of Weber State University at http://physics.weber.edu/schroeder/fluids/ proved to be extremely valuable in this project. With the help of these resources among others, I also acquired a bird's-eye view of LBM and the fluid simulation scene as a whole: there was the top-down approach of discretizing the NS equations, there was the completely microscopic viewpoint of Smoothed Particle Hydrodynamics which turns out requires simulating and tracking the motions of an unimaginably humongous number of fluid molecules to be of any practical use for dense fluids such as water, and there was the LBM- a compromise between the macroscopic and the microscopic treatment of fluid motion, the so called "mesoscopic" approach. While complete description of the LBM technique is obviously not possible in a simple blog post as this, as must be evident by the books on the topic I've mentioned above, I will try to summarize how I implemented it in code.
In Lattice Boltzmann Method, space is divided up into 'lattice points'. Now depending on how many dimensions you want to work with, LBM can be 1D, 2D or 3D. This project is a 2D LBM implementation and thus the XY plane is used as the domain of simulation. The program I've written explicitly draws a specified number of regular rectangular grids on the plane. The centroids of the square cells so formed are taken as the lattice points to be assigned properties according to the LBM. Note that this definition of lattice point as the centroid of a cell is completely arbitrary, what matters is that their ordering(and if visualization is important, their spacing as well) be respected - the LBM from what I've understood working on this project, doesn't have a built-in assumption about the nature of lattice points, it is implementation-specific. Now, each lattice point, according to 2D Lattice Boltzmann, is given a set of particle distributions for each of 9 directions (this is called the D2Q9 scheme) : Rest, Eastbound, Northbound, Westbound, Southbound, NorthEastbound, NorthWestbound, SouthWestbound and SouthEastbound. It may be beneficial to observe the use of the term 'particle distribution' as opposed to individual particles in understanding, partly, why the LBM is called a 'mesoscopic' approach. Now, each of these distributions can be assigned a direction vector, together forming a unit circle. In simpler terms, each of the aforementioned particle distributions are assigned direction vectors: [0,0],[1,0],[0,1],[-1,0],[0,-1],[1,1],[-1,1],[-1,-1] and [1,-1] in order. In most literatures, the particle distribution (a scalar) is represented as f with a subscript denoting the direction it belongs to and the direction vector is represented as e with a subscript also denoting its direction, the subscript running from 0 to 8 for each of the nine directions. Besides these quantities, there are also the so called weights denoted as w associated with each direction.
The basic idea in the Lattice Boltzmann Method is that particle populations in all the lattice sites undergo two steps: streaming/propagation and collision/relaxation. Streaming aims to emulate the transfer of properties throughout the fluid whilst collision is an approximation of the tendency of the fluid to equilibriate(read settle down). The heart and soul of this treatment is statistical mechanics as I mentioned before and the so called Lattice Boltzmann Equation, aka LBE in the literature. Motivation for the streaming step may be obvious if we are to have any chance at emulating a transport phenomenon where properties such as velocity and density are pushed around but the collision step may warrant a short explanation. If oversimplification is no concern, basically the motivation for collision is that properties of particles that are further away from the equilibrium/average values are gradually shifted towards the equilibrium. This is also why this step is also called the relaxation phase: properties that are away from the norm ease into their equilibrium values. From a molecular perspective, collision between molecules does push the overall state of the system towards an equilibrium and a state of homogeneity/isotropy.
Streaming just transfers one cell's particle populations/distributions to its appropriate neighbors. The term 'appropriate' serves to encapsulate the idea that a cell that is streaming away its particles to its eight neighboring cells does it in the following rather intuitive way: the Eastbound particle distribution f0 replaces the eastern neighbor cell's Eastbound particle distribution and so on for all the eight directions; the rest population is not streamed anywhere. This is done with all the cells in the grid but you have to be careful not to overwrite information on a neighboring cell that still needs to be used for streaming from that cell to its neighbors. So what is typically done is two copies of the grid's cells with all their information are made and one of the copies is updated with stream information from the other which remains unchanged throughout the process. This is important because streaming is supposed to be a simultaneous process. Now, what I've just described is for interior cells(I've been using the term cell and lattice point interchangeably) meaning a cell that has all its neighbors as actual fluid cells. Here, I should explain what a fluid cell is versus what a non-fluid cell is. In real life, you'll want to see how a fluid flows around an obstacle. So, we need a way to represent these barriers that do not allow flow to pass. What is typically done is the grid cells that are supposed to be these obstacles are marked in some way, if you implemented a cell as a class, maybe you could give it a descriptive property : maybe a boolean variable called isSolid. Anyway, you know which cell is a fluid and which isn't, however you implement it in code. Now any cell that is surrounded by actual fluid cells (with isSolid property set to false, say) is an interior cell and the aforementioned process of streaming holds good. But if any of its neighboring cells is a solid cell(an obstacle), you perform a so called 'bounce-back'. It is pretty simple: the cell that is streaming its particles upon encountering a solid neighbor gets back the same particle distribution but in the opposite direction. If you had a cell undergoing streaming with a solid northeast neighbor, upon streaming the northeastbound particles f5 to it, the streaming cell itself gets its northwestbound distribution f7 's value changed into the value of the f5 it was trying to stream instead. The neighboring solid cell doesn't undergo any change as should be obvious. Hence, the term bounce-back. Now, there seems to be two versions of the 'bounce-back' approach to solid boundaries, namely the full bounce-back and the halfway bounce-back but at its simplest, this is how it works and indeed how it's implemented in my code. It is worth pointing out that the bounce-back boundary translates to the macroscopic no-slip condition of fluid flow.
Now, onto the collision step. Collision, in the broadest of sense, being an easing into some kind of equilibrium, has a number of different approaches. The simplest of these seems to be the BGK (Bhatnagar-Gross-Krook) collision process which works as follows. You calculate the equilibrium particle distributions fieq for all the nine directions (i=0 to 8) using an expression derived from, it seems, the Boltzmann distribution of particle velocities. No further knowledge of the actual physics of this particular distribution is required to implement it in code. The expression is as follows:
Here, the weights wi are the constants 4/9 for i=0(rest direction), 1/9 for i=1,2,3,4(E,N,W,S) and 1/36 for i=5,6,7,8(NE,NW,SW,SE). If I understand correctly, these values are what they are if the conservation of mass and momentum is to be satisfied in collisions. Density ρ is the cell's density calculated as:
c is the speed of sound and is usually taken as unity. The vector ei is the direction vector pertaining to the direction i as mentioned a few paragraphs above i.e. [0,0] , [1,0], [1,1] and so on. The vector ui is
the actual velocity vector of the cell calculated as:
After the equilibrium particle distributions fieq have been calculated for all nine directions, the relaxation equation as given by BGK is used:
Here, 𝝂 is the viscosity term supposedly to be between 0 and 2. If the multiple fi terms look confusing, all this equation means is you perform the operation on the right hand side and update the value of fi for each direction i.
Okay, having explained the working equations of the collision operation, it is important to observe that it is a wholly local process i.e. no neighboring cell's information is used here. Sure, the particle distributions will be changing with time because every fluid cell will be streaming to every other fluid cell and thus changing the macroscopic properties of density and the velocity but the collision itself is dependent only the cell's current properties.
That's all about the two steps of the LBM algorithm. But there's still an important aspect left to explain: domain boundaries. Since we're only simulating in a small region of space, we must specify how the fluid behaves at the interfaces: the top, bottom, left and the right boundaries. Usually, we want these to be open boundaries for a freely flowing fluid. More often than not, the left boundary is the inlet from where the fluid flows into our system. As such, it makes sense to hold the inlet column of cells at such particle distributions that upon calculating their macroscopic parameters, densities and velocities, they amount to a constant of our choosing. In my code, I've set the incoming fluid's density as 1 and the velocity something lower than or equal to 0.3. LBM seems to be unable to cope with velocities near the speed of sound c(usually taken 1), so anything over 0.3 is liable to render the simulation unstable. So, the first column of our fluid cells are constrained to a constant velocity and density, meaning they are not streamed into. Now, the way to calculate the particle distributions is actually using the first expression, that for fieq . We calculate these for all the directions for our choice of velocity and density and assign them to the inlet cells and we don't touch them as far as modifying their distributions is concerned. Information flows from these cells, not to them.
Then the last column of cells. We can do two things here. We can either impose a so called 'periodic boundary' or a 'static boundary'(I made this up, dunno if that's the actual term). In a static boundary approach, we assign to the last column of cells, the outlet cells, the values of the cells immediately to their left. (At this point, you should know whenever I'm talking about values, it's the particle distributions fi.) This is supposed to pretend that there's no longer a variation in the flow properties between the columns of cells near the outlet and they're infinitely far from whatever obstacles our system may have. The alternative is 'periodic boundary' where our code pretends that the column of cells immediately to the right of the outlet cells is in fact our first column of cells, that is the domain behaves like a loop from back to the front. In this case, the inlet column of cells would in fact be streamed into from the last column and so on as if they were no different than any other column of interior cells. When I tried this, the simulation was way too unstable for my taste so I stuck to the static boundary approach.
Now for the top and bottom boundaries, the most common approach is to apply the periodic boundary to them both so that the top wraps back to the bottom row of cells when they try to stream to the cells above and vice versa for the bottom row of cells. And this is what I did in my code.
As far as the initial conditions are concerned, each cell may be initialized with a particle distribution according to the required inflow fluid velocity OR with zero velocity. I've found better results when initialized with the inflow velocity.
Putting it all together, we have a simple algorithm when done right produces amazing looking fluid animations. The steps I've followed in my code is: initialize all the cells, collision, streaming, calculate the cell's macroscopic parameters, output, repeat from collision.
I think I've explained the general method mostly completely. Now, I'm going to briefly describe my specific implementation in JavaScript. The cells are represented as an array of rows, each row being an array of cells of the row. Each cell is an instance of a Cell class. Each cell instance stores its own particle distribution as an array, its macroscopic velocity and density and a flag as a marker for whether it is a solid obstacle. There's also the weights and the direction vectors that really are constants and really should've been static members seeing as they don't differ between instances but I am under the impression that JavaScript doesn't yet have full support for static members in classes. The grid has its first and last rows and columns as boundary cells (read dead cells) that have nothing to do with the actual fluid or obstacles but are there just for visualization reasons and are marked as green cells (at least as of this writing); we do not iterate through them in the algorithm. For convenience, from here on out, I will thus refer to the second rows and columns as the first and the penultimate rows and columns as the last.
The first column of cells is initialized with the required inflow velocity's corresponding equilibrium particle distributions. This is our inlet/inflow column. This column is unconditionally assigned the color red. Depending on a switch, the rest of the other cells are either initialized to a particle distribution corresponding to zero velocity or the same inflow velocity as the first column. Personally, I favor initializing every cell to the inflow velocity's corresponding distributions.
After initialization is done, I perform the collision step, followed by the streaming process on all fluid(non-solid) cells, except those on the first column(the inlet column). Why the exception? I implement a fixed inlet boundary condition i.e. the inlet column never changes its properties and is never streamed into, and collision would have little effect since it always is at the equilibrium distribution fieq corresponding to the specified inflow velocity.
A little detail regarding the streaming process: there's two possibilities for implementing this - iterate through all the fluid cells and stream out from them to their non-solid neighbors OR iterate through all the fluid cells and stream into them from their non-solid neighbors. At first, I inadvertently wrote the first kind of streaming procedure and then later, I rewrote it as the second kind. The second kind turned out to be shorter and I think a bit more efficient. Think of it as pulling the distributions from the respective neighbors into the cell and keeping it as its own(in the same direction). In case of a solid neighbor, there's nothing to pull from there, so the distribution in the direction of the neighbor is reflected right back to replace the cell's distribution in the opposite direction.
The open boundaries are: fixed inlet boundary, static outlet boundary, periodic top and bottom boundaries. For the fixed inlet boundary, the first column's cells are held at a constant equilibrium particle distribution corresponding to the specified inflow velocity and never changed throughout the simulation. Streaming doesn't occur into these cells and collision is pointless for these cells since all collision does is push the distributions towards the equilibrium anyway. For the static outlet boundary, the final column's(outlet/outflow column) distributions are copied from that of the column to the immediate left. The upper and lower boundaries loop back to each other in that 'above' for the first row is defined as the last row and 'below' for the bottom row is defined as the first row.
After collision and streaming, finally each cell's macroscopic parameters, density and velocity, are calculated according to the second and third expressions given a few paragraphs above.
Finally, while drawing it out on the canvas, the velocity's y component is inverted in sign since computers assume the origin to be at the top left corner. And a few other cosmetic manipulations for a more sensible visualization are made before actually doing the painting.
The end result is a visually pleasing animation in the web browser.
References:
among others.