Realtime Covid-19 spread modelling

This is an upgrade to the previous project. Instead of taking hypothetical values for the SIR model parameters, this program retrieves the latest (daily) time series data for the Coronavirus pandemic from https://pomber.github.io/covid19/timeseries.json and simulates how the infection might play out in the future. The time series data is used to get an estimate of the SIR parameters β (the "contact rate" constant) and α (recovery constant). These vary enough through time to cause wild variations in the model outcome. So, I've included the option to use the latest, the minimum, the maximum and the mean values, out of which the mean seems to give the most sensible looking graph. The way the parameters are estimated is basically using two (shorter) of the three governing equations of the model:
delS/delT = -β*S*I/N
delI/delT = β*S*I/N - α*I
delR/delT = α*I
from where,
β = delS/(I*S/N)
α = delR/I
where delT = 1 day, since that is how frequent the available data is.
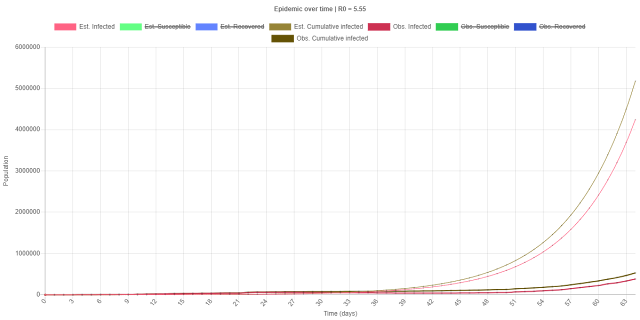
Now, the Susceptible population S, Infective population I and the Removed population R aren't available as such. The time series data source mentioned above gives the daily recorded data for each country since Feb. 22, 2020. This is converted into a global daily record time series data by summing over all the countries. The final form looks something like this, and this is for a particular date:

1. date: "2020-3-26"

1. confirmed: 529591

1. deaths: 23970

1. recovered: 122149

The 'confirmed' value corresponds to all the active infections (which meets the definition of the infective population in our model) + the 'deaths' + the 'recovered' values.

So, for the infective population, I = confirmed -  deaths - recovered

and for the susceptible population, that's the global population minus the people who are still in active infection and those who've recovered or died combined i.e. S = N - confirmed

I tried doing a simple power-law function fitting for the alpha and beta parameters using the Least Square Technique (LST) here but ultimately decided against using it in the model as I thought their time-evolution should be more logistic-like rather than monotonous. For that spreadsheet, I used data attributed to Mathemaniac after watching his video

Perhaps I could use the latest 5-day or 14-day averages for better estimating the model parameters. The model would do even better if I could figure out β(t) and α(t) for the entire duration of the epidemic since the parameters seem to be constantly fluctuating IRL.

Anyway, here is the code.

Edit: I've removed the (flawed) max/min parameter estimation and added last 5 and last 14 data based parameter estimation. Doesn't seem to do much good.
Edit: I've only now realized that web apps that don't require/have a back end i.e. web pages that don't require server-side coding can be hosted on GitHub itself! I have thus pushed this project to GitHub as a repository. The corresponding GitHub Pages site is here. I will be pushing all future JavaScript web apps directly to GitHub as repositories of their own; no more GitHub Gist for such programs. All update to the apps will be applied to their corresponding GitHub repositories, not their Gists. I will also be shortly porting all my past JavaScript web apps in this blog that I'd uploaded to GitHub Gist to GitHub as repositories.